한 칸씩 쌓기

프랜시스 골턴과 골턴 보드: regression toward the mean

- 프랜시스 골턴은 유전을 통해 형질이 발산하지 않는 것(키 큰 부부의 자녀들이 더 키가 크지 않고 부부보다 오히려 작은 현상)이 유전이 갖는 물리적인 특성이라고 추측했다.

- 다시 말해, 평균으로의 회귀가 이런 유전의 특성이 가져오는 인과적인 결과로 해석했다.

- 이 해석은 (당연히) 잘못된 해석이지만, 골턴의 regression을 해석하기 위한 접근은 최초로 상관관계(correlation)라는 개념을 탄생시켰다.

Galton and the Abandoned Quest

작가의 주장

- 골턴과 피어슨의 주도로 진행된 통계학의 발전은, 통계학계를 model-blind data-reduction 단체로 만들어버렸다.

- correlation의 발견과 고도화에만 집중한 나머지, causality의 발전은 경시되고 낙후될 수 밖에 없었다.

Pearson: The Wrath of The Zealot

- 피어슨은 상관관계가 전부고, 통계학과 과학이 추구해야할 것은 상관관계를 검증하는 것뿐이라고 강조했다.

- 피어슨은 인과관계란 두 모집단(변수)을 부적절하게 조합했을 때 발생하는 잘못된 해석이라고 주장했다.

- 피어슨과 그 제자들이 당대 통계학의 주류였고 그들은 인과관계에 매우 적대적이었기 때문에, 오랜 세월동안 라이트가 반론을 제기하기 전까지 인과관계에 대한 연구는 매우 미미했다.

Sewall Wright, Guinea Pigs, and Path Diagrams

- 라이트는, path diagram을 활용해 기니피그의 털 색깔이 어떻게 유전되는지를 연구했고, 인과 모델과 통계학을 조합한 최초의 연구사례를 남겼다.

- 하지만, 당대 주류인 통계학계로부터 무수히 많은 공격을 받았다.

- 당시 공격하는 사람들의 논리

    - 인과 모델을 그래프로 표현하는 것은 불가능하다.

    - 인과 모델이 맞는지를 검증할 수 없기 때문에, 이를 현실에 적용하는 것은 신뢰할 수 없다.

- 라이트의 주장:인과 모델(가설) 없이는 인과 관계 해석(발견)은 불가능하다.

    - 처음 도안한 인과 모델(가설)이 잘못되었음이 데이터로 검증되면, 다른 인과 모델(새로운 가설)로 검증하면 된다.

    - 라이트의 연구 방법론은 상관관계에서 인과관계를 뽑아내는 게 아니라, 가설과 상관관계를 조합하여, 어떤 인과 현상을 설명하는 것

E PUR SI MUOVE (And Yet It Moves)

출산시 기니피그 무게에 대한 예시

- 자궁에서 67일 보낸 태아가, 66일 보낸 태아보다 5.66g 더 무겁다.

- 결론: 하루에 5.66g씩 자라는가? 

- No! 

- 이전의 무게와 자궁의 크기 등이 주는 요인들이 있다.

- 이를 인과 그래프로 표현하고 계산하면 하루에 몇 g씩 자라는지 규명 가능하다. (연립 방정식 문제로 치환된다.)

라이트는 통계학이 단순히 방법론의 집합이라는 피셔의 주장을 극혐했다.

- 방법론뿐만 아니라 데이터가 어떻게 생성되는지(인과 모델)에 대한 이해를 통합해야 한다고 주장했다.

주류 통계학은 모델을 가정하지 않고 데이터를 통해서도 (잘 가공만 하면) 과학적 인사이트를 도출할 수 있다고 주장했지만, 필자는 이런 식의 "모델 없는" 데이터 해석은 1단계 수준의 인과 추론만 가능할 뿐, 더 높은 단계로는 갈 수 없다고 주장한다.

From Objectivity to Subjectivity - The Bayesian Connection

- 상관관계 해석을 포함한 다른 주류 통계학과 달리, 인과 추론은 분석가에게 주관적 해석을 요구한다.

- 베이지안 분석론: Prior Belief + New Evidence -> Revised Belief

     - 베이지안 분석론의 장점은, 데이터 양이 많아지면 결국 하나의 객관적인 진실로 우리의 믿음을 수렴시킬 수 있다는 것이다.

- 그동안 인과추론 연구가 배척받아 왔기 때문에, 다른 분야 대비 방법론을 적용하고 설명하는 데에 필요한 언어가 부족하다.

- 이런 언어들이 향후 챕터에서 더 소개될 예정

하나님은 아담에게 "선악과를 먹었느냐"고 Yes/No 답변을 요구했다. (사실 관계를 질문)

아담은 "이브가 선악과를 줬다"고 원인을 답변했다.

마찬가지로 하나님은 이브에게 "아담에게 선악과를 주었느냐"고 Yes/No 답변을 요구했다. (사실 관계를 질문)

이브는 "뱀이 날 유혹했다"고 원인을 답변했다.

창세기 선악과 이야기에서 작가가 읽어낸 3가지 함축

1. 세상은 단순한 사실관계(dry facts)로만 이루어지지 않고 모든 일들은 거미줄처럼 인과관계가 얽혀있다.

2. 인과관계 설명은 우리의 지식 대부분을 구성한다.

3. 인과관계를 추론하는 것은 도약(a leap)이 필요하지, 데이터로부터 자연스럽게 발생하지 않는다.

    - 기계학습에서도 마찬가지일 것이다. 데이터를 아무리 많이 학습해도 기계는 설명을 도출하지 못한다. push (인과 구조도, 도메인 지식등)가 필요하다.

    - 인류는 선악과(push)를 먹었다.

The Three Levels of Causation

"인과관계란 무엇인가?" 같은 철학적이고 형이상학적인 토론에서 벗어나, 인과 관계를 실제로 적용하기 위한 좋은 질문은 "인과 추론자 (causal reasoner)는 무엇을 하는가?"이다.

다시 말해, 인과추론이 가능한 모델이, 불가능한 모델이 할 수 없는 일 중 가능한 것은 무엇인지를 정의하는 것이다.

인과 추론자의 능력에 따라서 3가지 레벨로 나눈다. (위로 올라가는 질문에 답변 가능할수록 능력이 좋은 인과추론자이다. - 왜 능력이 좋은지는 추후 설명)

1. Association

- Seeing, Observing

- 예) 올빼미는 밤에 움직임을 관찰해서 쥐가 있을 것을 예상하고 달려든다. 알파고는 수백만개의 데이터를 통해 승리하는 패턴을 발견하고 수를 둔다.

- Association이 가능한 인과 추론자는 "What if I see ...?" 질문에 답변할 수 있고, 이는 "예측 (Prediction)"을 가능하게 한다.

- 전통 통계학에서는 이를 가능케하는 방법론들(상관분석, 회귀분석)이 다수 존재

- 하지만 인과관계는 밝혀낼 수 없다.

    - ex) 치실 구매가 증가하면 치약 구매가 증가한다는 것은 알 수 있지만, 인과관계는 알 수 없다.

2. Intervention

- Doing

- Association과 달리, X를 했을 때 Y가 어떻게 달라지는지를 답변할 수 있다.

- 개입의 결과를 예측하는 가장 직접적인 방법은 "실험"

- "실험"에 필연적으로 세팅되는 인과 모델을 통해 "What if we do ...?" 질문에 답변할 수 있어진다. -> 이는 미래를 바꿀 수 있게 해준다.

3. Counterfactuals

- Imagining, Retrospection, Understanding

- 과거를 변경해야 하는 어려움이 있다. - 데이터는 Fact이기 때문에 Counterfactual을 구하기 위해서는 상상을 동원해야 한다.

- 그동안 과학이 발전한 방식

    - ex) 스프링에 가해지는 무게가 2배가 되면, 스프링의 길이도 2배가 될 것이다. (훅의 법칙)

- 변수들 사이 관계가 함수로 표현 가능해진다.

Causal Model의 중요성

- 유발하라리: 인류는 "인지 혁명"이라 일컫는 "상상력"을 통해 진보해왔다.

- 실험만으로는 Why라는 질문에 답변할 수 없다.

- 데이터와 실험 결과를 구조화하는 causal process (때로 이론, 자연법칙으로 불린다)가 있어야 Why에 답변할 수 있다.

- 한층 더 나아가, 이런 이론과 자연 법칙을 부정하는 것도 이런 causal process의 일부다.

The Mini-Turing Test

기계가 인과 추론 능력을 어떻게 획득할 수 있을까? (매우 어려운 문제)

-> 기계 (또는 인간이) 인과 추론 능력을 어떻게 표현할 수 있을까? (덜 어려운 문제로 치환)

    1. 필요한 정보 획득

    2. 질문에 정확이 답변

    3. 알고리즘에 의해 함

예시

• CO: Court Order (법원 명령)
• C: Captain Order (지휘관 명령)
• A: soldier A shot (병사 A가 총 발사)
• B: soldier B shot (병사 B가 총 발사)
• D: prisoner death (죄수 죽음)

1. Association

- 죄수가 죽음과 법원 명령은 연관 관계가 있는가? -> Yes 답변 가능

- A가 발사한 것과 B가 발사한 것은 연관 관계가 있는가? ->Yes (둘 다 동시에 발사하거나, 발사 안 한다) 답변 가능

2. Intervention

- 만약 병사 A가 지휘관 명령을 어기고 무조건 발사하겠다고 결심한다면? (규칙 위반)

    - 기계에게 인과관계를 가르치려면, 규칙을 어떻게 어겨야 하는지 (규칙 위반을 통해 인과 관계를 어떻게 발견할 수 있는지) 가르쳐야 한다.

    - 기계에게, 특정 이벤트의 발생 가능성을 통제(개입)할 수 있다고 알려주는 것은, 해당 이벤트로 들어오는 화살표를 모두 제거하고 분석을 진행하는 것을 의미한다.

- 만약 병사 A가 지휘관 명령을 어기고 무조건 발사 안하겠다고 결심한다면? (규칙 위반)

    - 법원 명령이 떨어지면, 병사 B는 발사할 것이기 때문에, 죄수 죽음은 결국 일어날 것이다.

    - CO 때문에 D가 발생했다를 파악해야만 mini-Turing test를 통과할 수 있다.

데이터만으로는 인과관계를 잘못 해석할 수도 있다.

예시

• 백신 접종률: 99%
• 백신 접종시 부작용 발생확률: 1%
• 부작용 발생시 사망확률: 1%
• 백신 접종시 천연두 발생확률: 0%
• 백신 미접종시 천연두 발생확률: 2%
• 천연두 발생시 사망확률: 20%

- 확률만 보고 인과 구조를 파악하면, 백신 접종이 더 좋은 선택지라는 것은 당연하다

- 하지만 실제 데이터는 다음과 같다.

• 백만명 중 99만명이 백신 접종
• 99만명 중 9,900명이 부작용 발생
• 9,900명 중 99명 사망
• 백신 미접종 1만명 중 200명 천연두 발생
• 200명 천연두 발생자 중 40명 사망

백신 접종으로 인한 사망자 99명이 천연두 발생으로 인한 사망자 40명 보다 많다.

-> 백신 접종은 잘못된 선택?

Counterfactual을 적용해보자

• 백만명이 전부 백신 미접종이라면?
• 백만명 중 2만명 천연두 발생
• 2만명 천연두 발생자 중 4000명 사망

백신 미접종자가 많을 수록 사망자가 더 많다.

-> 따라서 백신 접종은 좋은 선택

인과 모델은 확률을 수반한다.

X -> Y 관계에서 화살표는, X가 변했을 때, Y가 어떻게 바뀌는지에 대한 규칙 또는 함수를 함축한다.

On Probabilities and Causation

철학자들은 그동안 인과관계를 확률을 통해 정의하려 했다.

"확률 증가": X가 Y의 발생확률을 높이면, X는 Y의 원인이다.

직관적으로는 그럴듯하지만, 그동안 인과관계를 나타내는 데에 계속 실패해온 정의이다.

수식으로 쓰면 다음과 같다.

P(Y|X) > P(Y)

하지만, 인과관계가 아닌 상관관계일 때도 해당 수식은 성립한다.

아이스크림 판매량이 증가하면, 익사 사고가 증가한다. - 기온 상승이라는 "외부 변수"를 전혀 고려하지 못한 모델이다.

이에 따라 인과관계를 정의하려는 노력은, 이런 "외부 변수"를 제거하려는 데에 집중했다.

참고

이 책에서 작가는 인과관계를 정의하지 않는다. - 모든 정의는 오해석의 여지를 만든다.

대신, 인과관계 관련 주요 질문들을 답변하고, 해당 질문들을 답변하는 방법론에 집중한다.

(기하학에 관한 책에서도 점과 선을 굳이 정의하지 않고도, 기하학 문제들에 대한 답변들을 서술한다.)

외부 변수를 고려한 정의

P(Y|X, K=k) > P(Y|K=k)

하지만 해당 정의의 맹점은, 어떤 변수들이 K에 포함되어야 하는가?에 대한 질문을 답변하지 못한다는 것이다.

Nancy Carrwright는 1983년 이 맹점을 다파하는 정의를 다음과 같이 내렸다.

K에 포함되는 변수들은 Y와 "인과적으로 관계가 있는" 요인들이다.

하지만 해당 정의는, 인과 관계를 표한하기 위해 인과 관계를 가져다 쓴다는 비판을 받았다.

K에 포함되는 변수들에 대한 기준은 Chapter 4에서 자세히 다룰 예정이다.

작가는 do-operator를 활용해 이렇게 정의했다.

P(Y|do(X)) > P(Y)면, X는 Y의 원인이다.

확률론에 기반한 통계학이 세상의 수학적 표현을 가능하게 했다면, 인과 추론은 세상이 변했을 때 확률이 어떻게 변하는지를 파악할 수 있게 한다. (개입과 상상력의 힘으로)

Korea Summer Session on Causal Inference 2021을 듣고, 강의 내내 소개된 주다 펄 교수님의 The Book of Why를 구매했다.

한국 번역본이 없어서, 원서로 쿠팡에서 구매했다.

원서이기도 하고, 애초에 인과추론을 공부하기 위해 산 책인 만큼 챕터별 요약 및 독후감을 블로그에 남기고자 한다.

Intro. Mind over Data

서론

"causal inference"는 new science다.

- 인류는 "왜"라는 질문을 할 수 있었기에 진보했다. -> 이 질문을 학문적으로 접근하는게 "causal inference"

- 그동안은 "왜"를 표현할 수 있는 적절한 언어가 부재했다. -> "causal inference"가 시도한 것이 이를 수학적 언어로 표현한 것 -> 원인, 결과를 설명할 수 있는 과학족 도구가 된다.

- 데이터만으로는 의사결정을 할 수가 없다. -> 데이터를 해석할 수 있는 framework이 필요하고 "causal inference"가 이를 제공해준다.

"causal inference"의 두 가지 표현 방법 (언어)

1. causal diagram

- 점(변수)과 화살표(관계)로 이루어짐 -> 그리기 쉬움

2. mathematica equations

- 통계학에 기초

do-operator

: 특정 변수를 관찰에 그치는 것이 아닌 개입을 하는 (상상 or 실제의) 행위

- 전통 통계학에서는 표현하지 못한, 인과 추론에서의 핵심적인 개념

- 약물이 수명에 인과적인 영향이 있는지를 파악하기 위해서는 P(L|D)가 아니라, P(L|do(D))를 계산해야 한다.

    - P(L|D): 약물을 먹거나 먹지 않았을 때의 수명 (환자의 의지가 교란변수 (confounder)로 있을 수 있다)

    - P(L|do(D)): 약물을 강제로 먹이거나 먹이지 않았을 때의 수명 (환자의 의지를 제거한다)

A Blueprint of Reality

추론 엔진 (Inference Engine)은 3가지 input을 받는다.

: Assumptions, Queries, Data

3가지 output을 출력한다.

1. Whether given Query can be answered?

2. Estimand = mathematica formula (데이터로 Query의 정답을 도출하는 기작)

    - ex) 약물 X를 N 만큼 복용하면, 기대수명 E(L)을 f(X, N, L)만큼 높인다. => 여기서 f(X, N, L)이 Estimand

3. Estimate = f(X_real, N_real, L) (실제 Data로 구한 추정값)

    - uncertainty도 함께 출력

더 세부적으로는 아래 9개 과정을 거친다.

1. Knowldege

2. Assumptions

3. Causal Model

4. Testable Implications

5. Query

6. Can the query be answered? -> No: 2, 3으로 복귀

     -> Yes: find Estimand

     모든 Query가 answerable하지는 않다! 만약 외부 변수 Z가 D와 L에 모두 영향을 주는데도, Z를 계산에 포함 못한다면 Causal Model을 개선해야 한다.

7. Data

8. Statistical Estimation (<= Estimand w. Data) 

9. Estimate (Answer to Query)

이 구조도 없이 Data만 잔뜩 모으는 것은 "왜?"라는 질문을 절대 대답할 수 없다.

+ 이 구조도를 갖추고 있으면, 새로운 Data가 들어와도 예측이 가능하다. (일반적인 ML, DL은 그렇지 못한다. - 새로운 Data가 오면 함수를 새로 fitting해야 한다.)

추후 목차 소개

Chatper 1.

- 인과추론의 사다리: 관찰 -> 개입 -> Counterfactual

- Causal diagrams를 활용한 추론의 기초

Chapter 2. 

- Data에만 의존했던 지난 통계학의 맹점

- Sewall Wright: 최초로 Causal Diagram을 그렸던 유전학자

Chapter 3.

- Bayesian Networks 개념

- 왜 AI 분야에 Bayesian Networks가 중요한가

- 실생활을 Bayesian Networks로 표현한 예시

Chapter 4.

- RCT: Randomized Controlled Trial

= P(L|do(D))를 구하는 인류가 발명한 도구

Chapter 5.

- 실제 예시: Smoking -> Lung cancer

- Causal Question을 답하는데의 적절한 언어와 방법론의 중요성

Chapter 6

- Paradox 예시들: Monty Hall, Simpson, Berkson 등

- 인간의 직관은 인과적 추론에 기초하지, 통계적 추론에 기초하지 않는다.

Chapter 7

- 개입 (intervention)

- "causal inference engine"의 내부 기관들 설명

- back-door adjustment

- front-door adjustment

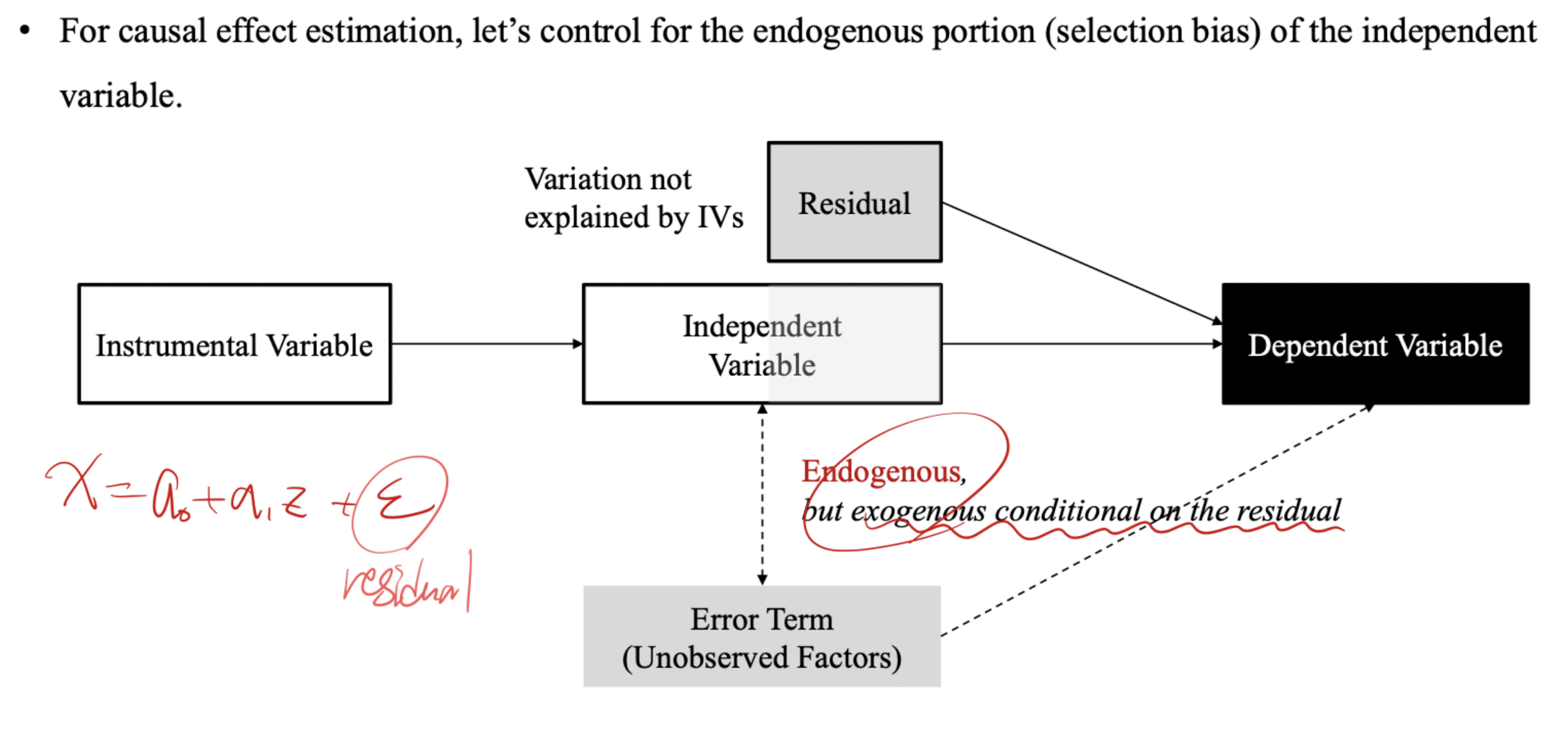
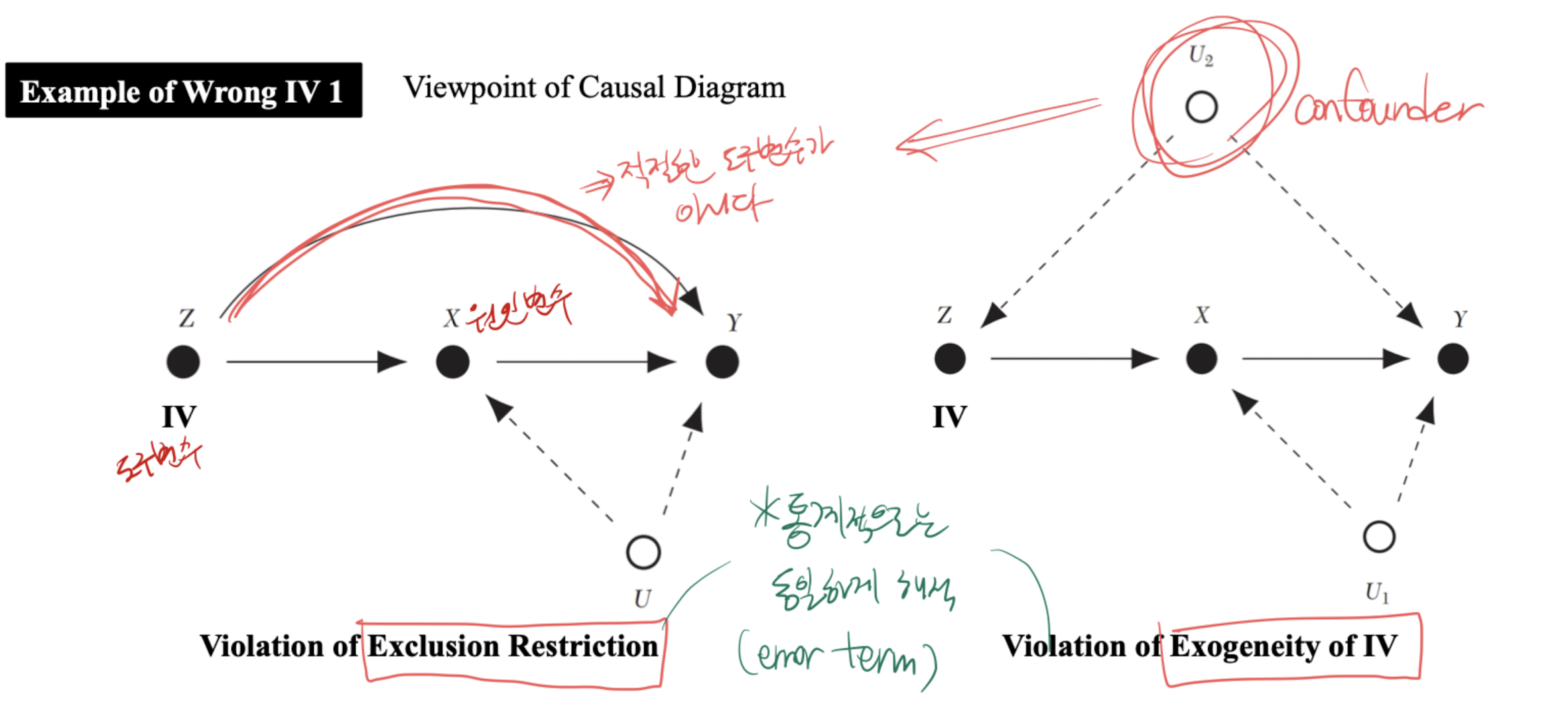
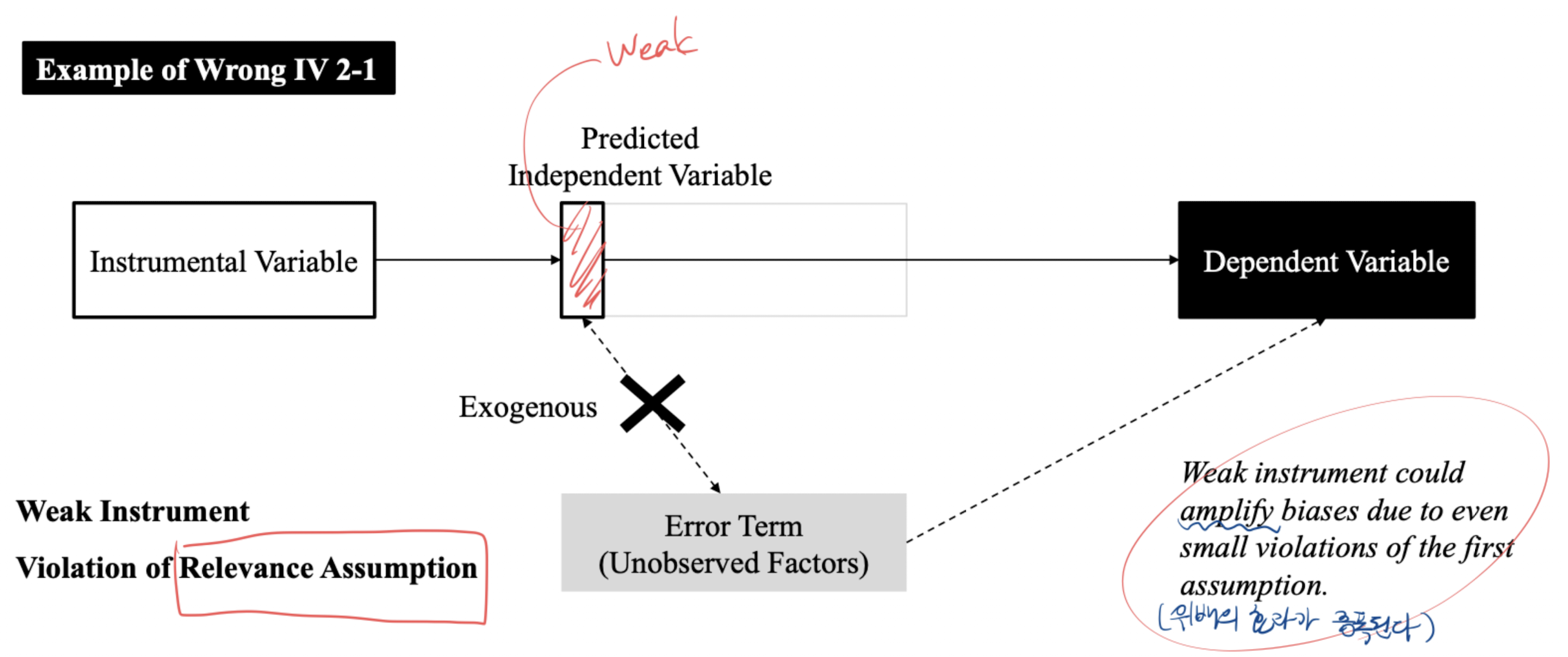
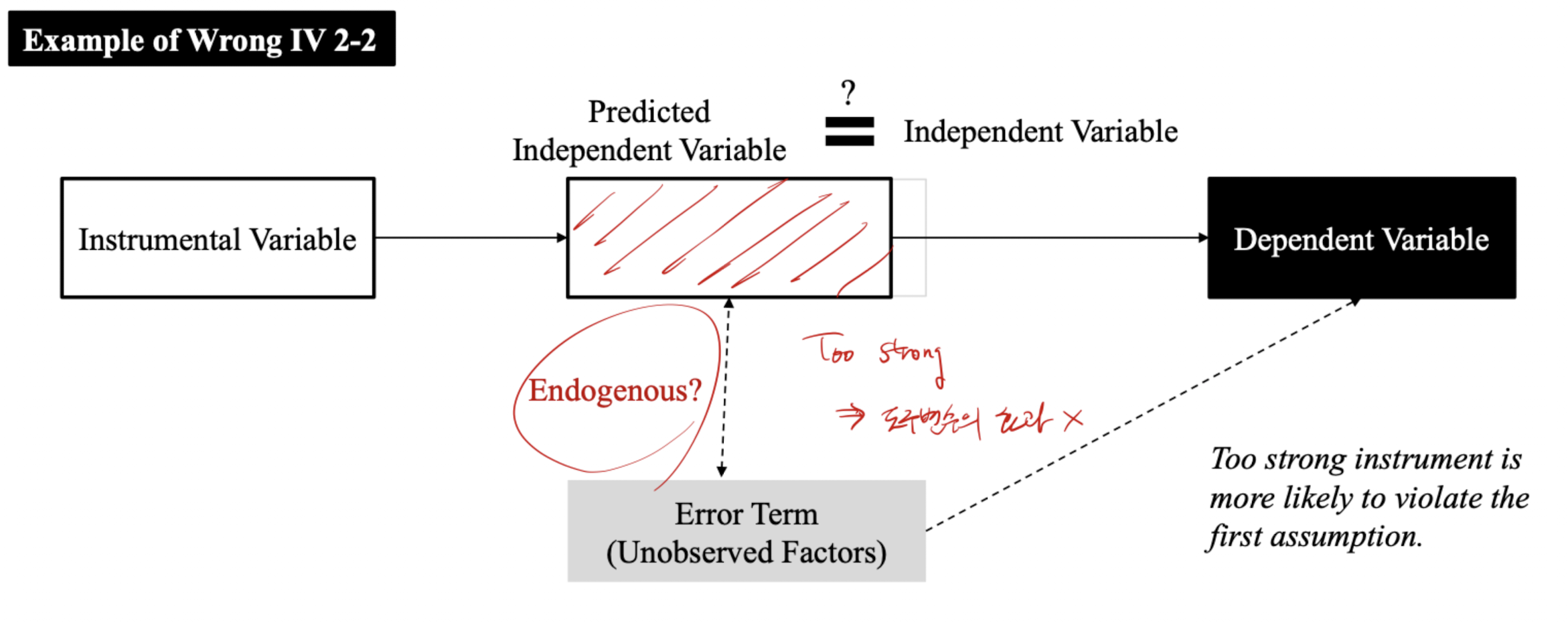
- instrumental variables

Chapter 8

- Counterfactuals

- "원인"은 "결과"에 "차이"를 만들어내는 것 + 그리고 그 "차이"는, "원인"이 없었다면 일어나지 않았을 차이여야 한다.

Chapter 9

- Mediation

- 원인이 결과에 주는 영향이 "직접적"인가, "간접적"인가

- 수학적 표현 방법과, 위 질문을 해결하는 인과추론 방법론들

Chapter 10

- AI와 인과추론

https://vwo.com/blog/multi-armed-bandit-algorithm/

요약

• Exploration만 하는 AB Test와 달리, MAB Test는 winner(혹은 이기고 있는 상태인 variation)에게 트래픽을 몰아준다
• winner를 일찍 결정해서 buisiness decision을 빨리 내릴 수 있다.
• AB test는 통계적 유의성을 확보하고 실험 종료 후 다양한 context에서 데이터를 해석할 때 주로 사용하고 MAB Test optimization algorithm으로 성공지표를 극대화하는 방안으로 실험이 진행된다.

Intro

What's Your Research Design?  

도구 변수 (Instrumental Variables)는 Treatment와 Control을 구분하기 어렵거나, 전/후 데이터를 관찰 못할 때 사용한다.

Causal Hierarchy of Research Design for Causal Inference

도구 변수는 Randomized Experiment나 Quasi-Experiment보다 그들을 바로 찾아내기 어렵기 때문에 사용하기 까다롭다.

Instrumental Variables

도구변수란 무엇인가? - 개념적 이해가 중요하다. (수식으로 엄밀하게 증명하는 것은 매우 어렵기 때문에)

Three Perspectives on Causation

• Potential Outcomes Framework: Systematic differences between treatment and control -> selection bias
• Structural Causal Model: Backdoor paths from unconditioning confounders or conditioning colliders -> noncausal association
• Statistics - Regression: Independent variable is correlated with the error term -> endogeneity

"selection bias, backdoor path 가 없다"는 통계적으로 원인변수와 error term 사이의 상관관계가 없다는 말과 동일하다.

Endogeneity (Selection Bias) in Regression

Endogenous (원인 변수와 error term 사이의 상관관계가 있음)하면 regression 결과를 인과관계로 해석할 수 없다.

하지만 현실에서 원인 변수를 완벽하게 Exogenous하게 통제하는 것은 불가능하다.

귀무가설은 모든 요인이 Endogenous 하다는 것이고, 별도의 처리를 통해 귀무가설을 뒤집는 것이 실험자가 할 일이다.

Taking the Selection Bias Out: Instrumental Variable (IV)

도구변수는 원인 변수(Independent Variable)에서 Exogenous한 부분을, Endogenous한 부분으로 부터 추출하기 위한 도구이다.

First Approach: Two-Stage Least Squares

1단계

- 원인 변수 X 중, Exogenous한 부분을 도구 변수 Z로 예측 ( X' = a_0 + a_1 * Z + \e )

2단계

- Z에 의해 예측된 X' 로 결과 변수 Y에 회귀적합

Second Approach: Control Function

원인 변수 중 Endogenous한 부분을 통제

X: 원인변수

Y: 결과변수

Z: 도구변수

v: Endogenous Term

Z와 v가 주어졌을 때, Y를 구하는 것이 목표

Example: Heckman Selection Models

Identification Assumptions for IV

1. 도구변수는 Error term과 상관관계가 없어야 한다.
2. 도구변수는 원인변수의 Endogenous한 설명변수와 상관관계가 있어야 한다.
   • 다시 말해, 도구변수는 원인변수에 대해 충분한 설명력을 가져야 한다.

Local Average Treatment Effect (LATE)

LATE: 도구변수에 의한 Average Treatment Effect

• Complier (도구변수가 1일 때, Treatment가 1인 변수들)에 대해서 도구변수로 계산한 Treatment effect를 Local Average Treatment Effect라 한다.
• LATE는 monotonicity assumption(Defier가 없어야 함)을 필요로 한다. 
• 도구변수의 한계: Complier에 따라 다른 도구변수는 다른 추정치를 낼 수도 있다.

다음 조건을 만족할 때, LATE = ATE

1. No always-takers
2. Homogeneity assumption
3. Randomness of IVs