Session 9. Instrumental Variables [9-1] 도구 변수 (Instrumental Variables)

Intro

What's Your Research Design?  

도구 변수 (Instrumental Variables)는 Treatment와 Control을 구분하기 어렵거나, 전/후 데이터를 관찰 못할 때 사용한다.

Treatment 와 Control 구분 못할 때 or 전/후 데이터 관찰 못할 때 Instrumental Variable 사용

Causal Hierarchy of Research Design for Causal Inference

도구 변수는 Randomized Experiment나 Quasi-Experiment보다 그들을 바로 찾아내기 어렵기 때문에 사용하기 까다롭다.

 

 

 

Instrumental Variables

도구변수란 무엇인가? - 개념적 이해가 중요하다. (수식으로 엄밀하게 증명하는 것은 매우 어렵기 때문에)

 

Three Perspectives on Causation

• Potential Outcomes Framework: Systematic differences between treatment and control -> selection bias
• Structural Causal Model: Backdoor paths from unconditioning confounders or conditioning colliders -> noncausal association
• Statistics - Regression: Independent variable is correlated with the error term -> endogeneity

"selection bias, backdoor path 가 없다"는 통계적으로 원인변수와 error term 사이의 상관관계가 없다는 말과 동일하다.

 

Endogeneity (Selection Bias) in Regression

Endogenous (원인 변수와 error term 사이의 상관관계가 있음)하면 regression 결과를 인과관계로 해석할 수 없다.

하지만 현실에서 원인 변수를 완벽하게 Exogenous하게 통제하는 것은 불가능하다.

귀무가설은 모든 요인이 Endogenous 하다는 것이고, 별도의 처리를 통해 귀무가설을 뒤집는 것이 실험자가 할 일이다.

Taking the Selection Bias Out: Instrumental Variable (IV)

도구변수는 원인 변수(Independent Variable)에서 Exogenous한 부분을, Endogenous한 부분으로 부터 추출하기 위한 도구이다.

도구변수(Instrumental Variable)와 원인변수(Independent Variable), Error Term 사이의 관계

First Approach: Two-Stage Least Squares

Two-Stage Least Squares

1단계

- 원인 변수 X 중, Exogenous한 부분을 도구 변수 Z로 예측 ( X' = a_0 + a_1 * Z + \e )

2단계

- Z에 의해 예측된 X' 로 결과 변수 Y에 회귀적합

 

Second Approach: Control Function

Conrol Function

원인 변수 중 Endogenous한 부분을 통제

Basic idea of control function

 

X: 원인변수

Y: 결과변수

Z: 도구변수

v: Endogenous Term

Z와 v가 주어졌을 때, Y를 구하는 것이 목표

Example: Heckman Selection Models

 

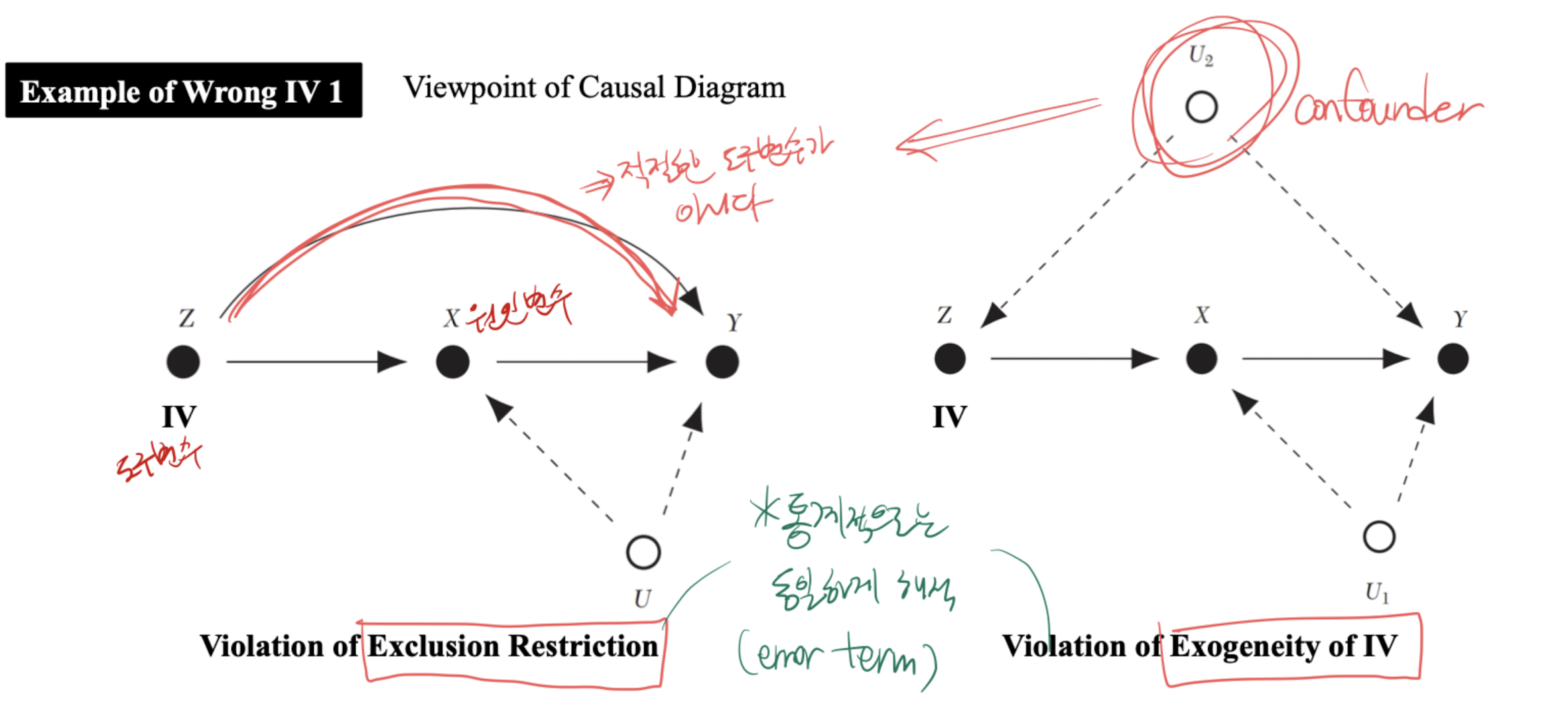
Identification Assumptions for IV

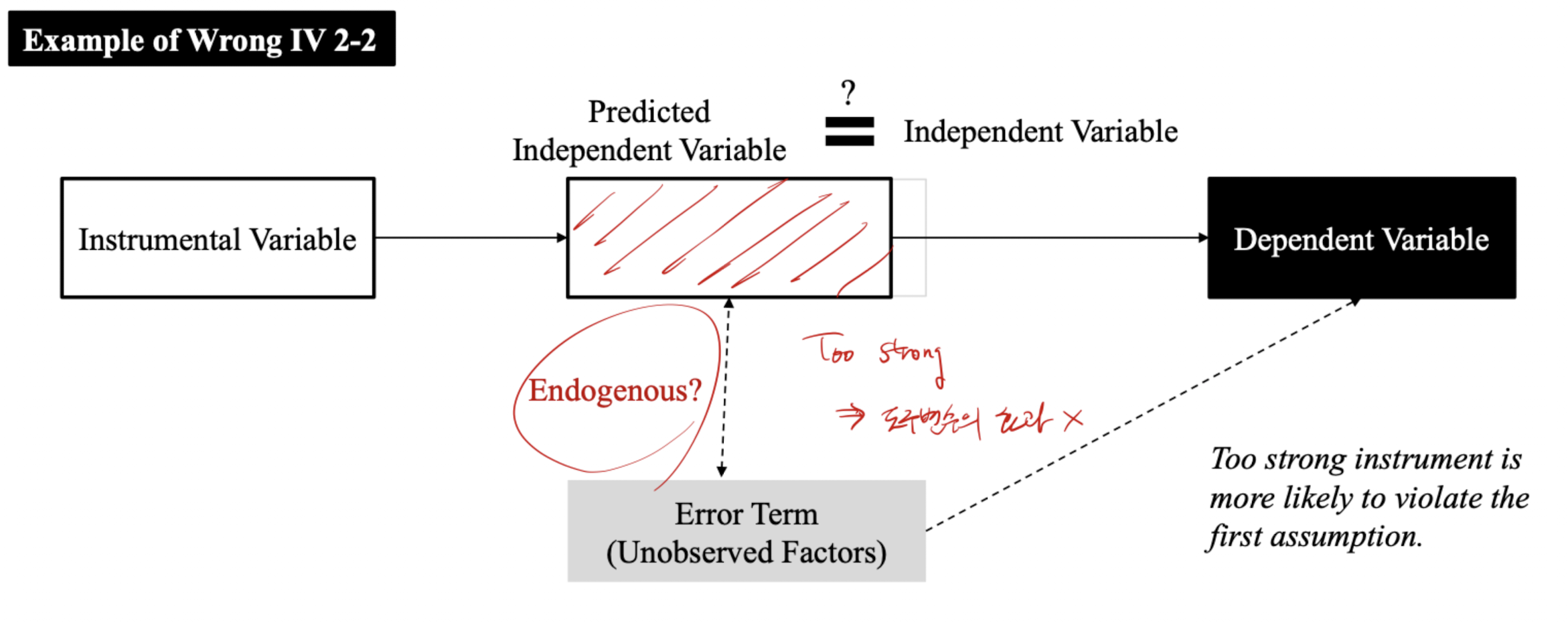
1. 도구변수는 Error term과 상관관계가 없어야 한다.
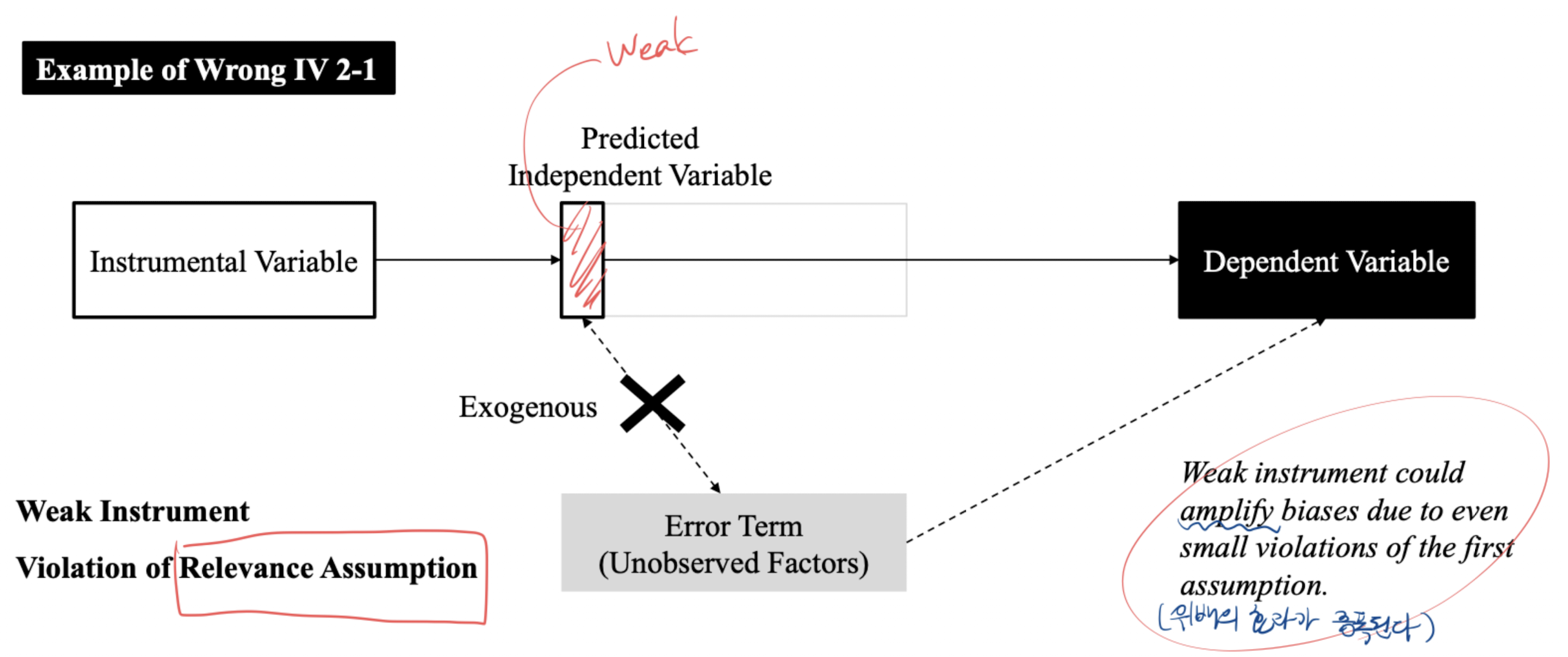
2. 도구변수는 원인변수의 Endogenous한 설명변수와 상관관계가 있어야 한다.
   • 다시 말해, 도구변수는 원인변수에 대해 충분한 설명력을 가져야 한다.

1. 도구변수는 Error term과 상관관계가 없어야 한다. - ex.1

1. 도구변수는 Error term과 상관관계가 없어야 한다. - ex.2

2. 도구변수는 원인변수의 Endogenous한 설명변수와 상관관계가 있어야 한다. - ex. Too Weak

2. 도구변수는 원인변수의 Endogenous한 설명변수와 상관관계가 있어야 한다. - ex. Too Strong

 

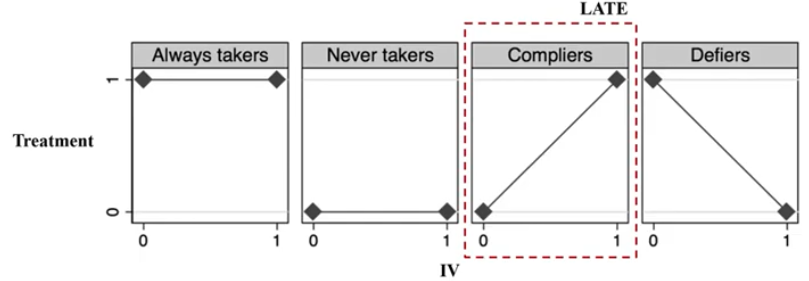
Local Average Treatment Effect (LATE)

LATE: 도구변수에 의한 Average Treatment Effect

• Complier (도구변수가 1일 때, Treatment가 1인 변수들)에 대해서 도구변수로 계산한 Treatment effect를 Local Average Treatment Effect라 한다.
• LATE는 monotonicity assumption(Defier가 없어야 함)을 필요로 한다. 
• 도구변수의 한계: Complier에 따라 다른 도구변수는 다른 추정치를 낼 수도 있다.

Always-takers, Never-takers, Compliers and Defiers

다음 조건을 만족할 때, LATE = ATE

1. No always-takers
2. Homogeneity assumption
3. Randomness of IVs